揭秘正数的补码：计算机内部的数字魔法

在计算机科学中，正数的补码是一个核心概念，尤其在处理整数运算和数字存储时显得尤为重要。理解正数的补码，不仅有助于深入掌握计算机内部的工作机制，还能为理解更复杂的计算机概念，如负数补码、溢出处理等打下坚实基础。本文将从补码的基本概念出发，逐步深入探讨正数的补码及其在计算机中的应用。

补码的基本概念

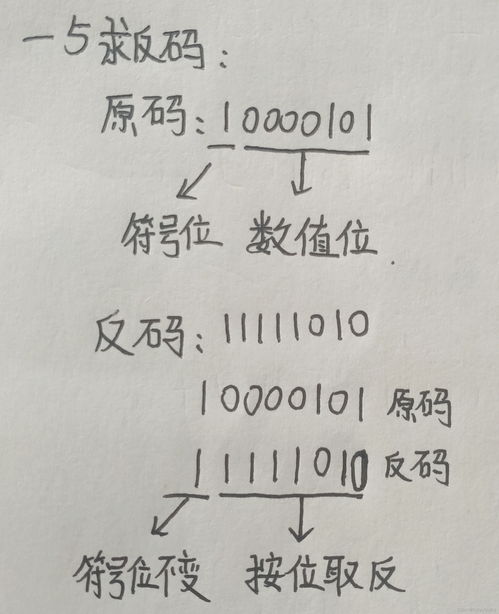
在计算机中，所有数据最终都被转化为二进制形式进行存储和运算。对于整数，常见的表示方法有三种：原码、反码和补码。原码即是最直观的二进制表示，正数的原码是其二进制形式，负数的原码是在其绝对值二进制形式的基础上，符号位（最左边的位）设为1。反码则是正数的反码与原码相同，负数的反码是其原码除符号位外每位取反。而补码，则是在反码的基础上加1得到的。

正数的补码特性

对于正数，其补码与原码是完全相同的。这一特性简化了正数的处理流程，因为在计算机内部进行加减运算时，可以统一使用补码形式，无需区分正负。例如，正数5的原码是00000101（以8位二进制为例），其补码也是00000101。这种一致性大大简化了硬件设计，提高了运算效率。

补码设计的优势

补码表示法的设计，不仅仅是为了简化正数的处理，更重要的是为了解决负数运算中的一些问题。在早期的计算机中，曾使用过原码和反码来表示整数，但这些方法在处理减法运算时显得尤为复杂。例如，使用原码进行减法运算时，需要先将减数取反（变为反码），再加1（变为补码），然后与被减数相加，步骤繁琐且容易出错。而补码表示法则直接避免了这一问题，无论是正数还是负数，都可以统一使用补码进行加减运算，大大简化了运算过程。

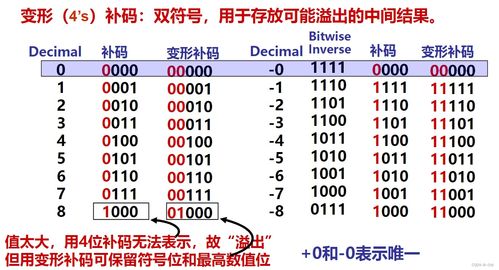
此外，补码表示法还能够有效解决溢出问题。在计算机中，由于存储位数的限制，当运算结果超出表示范围时，就会发生溢出。补码表示法通过特定的溢出检测机制，能够方便地判断出溢出情况，从而采取相应的处理措施。例如，在8位二进制补码表示法中，正数的最大值是127（01111111），负数的最小值是-128（10000000）。当运算结果超出这个范围时，就会发生溢出。通过检查运算结果的符号位和最高有效位，可以判断出是否发生了溢出。

正数补码在实际应用中的体现

正数补码在计算机中的应用广泛而深入。从最基本的算术运算到复杂的程序逻辑控制，都离不开补码表示法的支持。

1. 算术运算：在CPU的算术逻辑单元（ALU）中，所有的整数运算都是基于补码进行的。无论是加法、减法、乘法还是除法，都可以通过补码运算来实现。这种统一的处理方式大大提高了运算速度和准确性。

2. 条件判断：在程序执行过程中，经常需要根据某些条件来判断执行哪条指令或分支。这些条件判断往往涉及到整数的比较运算，而比较运算也是基于补码进行的。例如，判断一个数是否大于0，实际上就是判断其补码的最高有效位是否为0（对于正数，补码的最高有效位为0）。

3. 数据存储：在计算机内存中，所有的数据都是以二进制形式存储的。对于整数来说，无论是正数还是负数，都是采用补码形式进行存储的。这种存储方式不仅节省了存储空间，还提高了数据的读写速度。

4. 网络通信：在网络通信中，数据的传输也是以二进制形式进行的。为了保证数据的完整性和准确性，在数据传输过程中经常需要进行校验和纠错。而补码表示法由于具有简单、高效的特点，因此被广泛用于网络通信中的数据校验和纠错算法中。

补码运算示例

为了更好地理解正数补码在计算机中的应用，我们可以通过一个具体的例子来说明。假设我们有两个8位二进制正数A=5和B=3，我们需要计算它们的和A+B。

首先，将A和B转换为补码形式：

A的补码：00000101

B的补码：00000011

然后，将A的补码和B的补码相加：

00000101

00000011

00000111+ (注意这里没有发生进位溢出)

得到的结果00000111就是A+B的和7的补码形式。由于正数的补码与原码相同，因此我们可以直接将其视为原码进行解读。

结论

正数的补码是计算机科学中一个基础而重要的概念。它不仅简化了正数的处理流程，提高了运算效率，还为负数运算和溢出处理提供了有效的解决方案。通过深入理解正数补码的原理和应用，我们可以更好地掌握计算机内部的工作机制，为学习和掌握更复杂的计算机概念打下坚实的基础。同时，正数补码在计算机中的广泛应用也提醒我们，要时刻关注计算机科学的最新发展动态和技术趋势，不断更新自己的知识和技能储备，以适应不断变化的技术环境。