揭秘：扇形面积计算的三大关键公式！

在数学领域中，扇形作为圆的一个重要部分，不仅承载着几何图形的美丽，还蕴含着丰富的数学原理和计算公式。当我们谈及扇形的面积公式时，通常会涉及到三个核心的公式，这些公式从不同的角度揭示了扇形面积的计算方法，使得我们能够根据不同的已知条件，灵活求解扇形的面积。

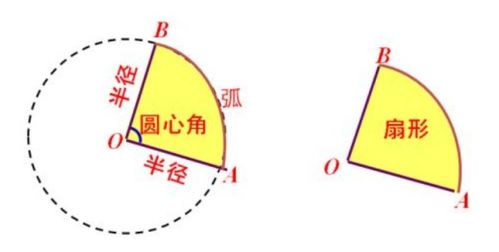
首先，我们需要明确扇形的基本概念。扇形是由圆上两点和连接这两点的圆内部分所围成的图形。这两点称为扇形的弧的两个端点，而连接这两点的线段称为扇形的半径。扇形的大小通常用其弧长占整个圆周长的比例来表示，这个比例称为扇形的圆心角，通常用弧度或度数来衡量。

接下来，我们逐一探讨扇形的三个面积公式。

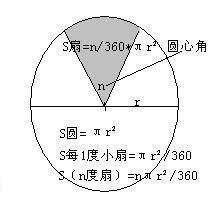
第一个公式是基于扇形圆心角的度数来计算面积的。这个公式是：扇形面积 = (圆心角的度数/360°) × π × 半径²。这个公式直接体现了扇形面积与圆心角、半径之间的关系。当圆心角为360°时，扇形即为整个圆，此时公式计算出的面积即为圆的面积。而当圆心角小于360°时，我们可以根据圆心角的度数占整个圆周长的比例，来计算出扇形的面积。这个公式非常直观，适用于已知圆心角的度数和半径时求解扇形面积的情况。

第二个公式则是基于扇形的弧长来计算面积的。这个公式是：扇形面积 = (弧长/2π×半径) × π × 半径²。这个公式看起来较为复杂，但我们可以将其简化为：扇形面积 = (1/2) × 弧长 × 半径。这个公式揭示了扇形面积与弧长和半径之间的直接关系。当我们知道扇形的弧长和半径时，可以直接使用这个公式来计算面积。这个公式的优点在于，它不需要知道圆心角的度数，只要知道弧长和半径即可。

第三个公式则是扇形面积与整个圆面积之间的关系式。由于扇形是圆的一部分，所以扇形的面积必然与整个圆的面积有关。这个公式是：扇形面积 = 圆的面积 × (圆心角的度数/360°)。或者，如果我们用弧度来表示圆心角，那么公式可以写为：扇形面积 = 圆的面积 × (圆心角的弧度/2π)。这个公式非常实用，因为它允许我们在不知道扇形具体形状（即弧长和半径）的情况下，通过知道圆心角和整个圆的面积来求解扇形的面积。这在处理一些复杂的几何问题时非常有用。

这三个公式虽然形式不同，但它们之间有着深刻的内在联系。它们都体现了扇形面积与圆心角、半径之间的关系，只是从不同的角度出发来揭示这种关系。在实际应用中，我们可以根据已知条件来选择最合适的公式进行计算。

例如，当我们知道扇形的圆心角的度数和半径时，可以直接使用第一个公式来计算面积；当我们知道扇形的弧长和半径时，可以使用第二个公式；而当我们知道圆心角和整个圆的面积时，则可以使用第三个公式。这种灵活性使得我们在处理扇形面积问题时能够游刃有余。

此外，这三个公式之间还可以进行相互转换和验证。例如，我们可以通过第一个公式计算出扇形的面积，然后通过第三个公式来验证我们的计算结果是否正确。这种转换和验证的过程不仅有助于我们加深对扇形面积公式的理解，还能提高我们的计算能力和数学素养。

除了这三个核心公式外，还有一些与扇形面积相关的推论和性质值得我们注意。例如，当两个扇形的圆心角相等且半径也相等时，它们的面积必然相等。这是因为扇形面积与圆心角和半径之间有着确定的数学关系，所以当这两个参数相等时，面积也必然相等。这个推论在处理一些与扇形面积相关的几何问题时非常有用。

此外，我们还可以利用扇形面积公式来解决一些实际问题。例如，在建筑设计中，我们可能需要计算某个扇形区域的面积来规划空间布局；在机械工程中，我们可能需要计算扇形零件的面积来确定材料用量；在地理测量中，我们可能需要计算扇形区域的面积来评估土地资源等。这些实际问题都要求我们熟练掌握扇形面积的计算方法，并能够灵活运用相关公式来求解。

综上所述，扇形的三个面积公式是数学中非常重要的工具。它们不仅揭示了扇形面积与圆心角、半径之间的深刻关系，还为我们提供了灵活多样的计算方法。在实际应用中，我们可以根据已知条件来选择最合适的公式进行计算，并通过相互转换和验证来确保计算结果的准确性。因此，熟练掌握这些公式并理解它们之间的内在联系对于提高我们的数学素养和解决实际问题的能力具有重要意义。