根号3的数值是多少

根号3是一个在数学和物理等多个领域中频繁出现的无理数。其值无法表示为两个整数的比，但可以通过几何构造或数值计算来求得近似值。根号3的具体数值为约1.7320508075688772935274463415059，下面我们将从几个方面来探讨根号3的含义、计算方法以及在各个领域中的应用。

一、根号3的几何意义

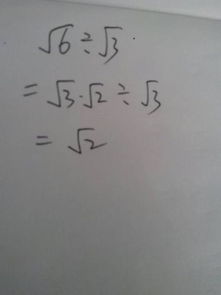
根号3在几何学中有着直观的解释。假设我们有一个等边三角形，其边长设为a，则可以通过构造一个高度h，来找到边长和高度之间的关系。由于等边三角形的三个内角都是60度，我们可以将一个顶点与对边的中点相连，形成一个直角三角形。在这个直角三角形中，斜边长度为a，一个直角边长度为a/2（对边的一半），另一个直角边长度就是我们要找的高度h。

根据勾股定理，有：

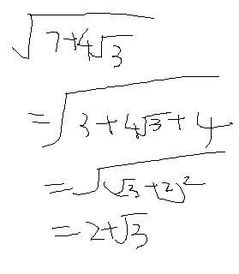
\[h^2 + \left(\frac{a}{2}\right)^2 = a^2\]

\[h^2 = a^2 - \frac{a^2}{4}\]

\[h^2 = \frac{4a^2}{4} - \frac{a^2}{4}\]

\[h^2 = \frac{3a^2}{4}\]

\[h = a \cdot \frac{\sqrt{3}}{2}\]

从上式我们可以得出，等边三角形的高h是边长a的根号3除以2倍。如果我们取边长a为2，那么高度h就是根号3。

二、根号3的数值计算方法

根号3作为一个无理数，其小数部分是无限不循环的。然而，我们可以使用各种数值方法来逼近其值。

1. 连续分数表示法：

根号3可以表示为连续分数的形式：

\[ \sqrt{3} = 1 + \frac{1}{1 + \frac{1}{2 + \frac{1}{1 + \frac{1}{2 + \dots}}}} \]

这种表示法提供了一种迭代逼近根号3的方法。

2. 牛顿迭代法：

牛顿迭代法是一种高效的数值求解方法，可以用来逼近根号3。设f(x) = x^2 - 3，我们需要找到f(x)的零点。从初始猜测值x0开始，迭代公式为：

\[ x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} = x_n - \frac{x_n^2 - 3}{2x_n} = \frac{x_n^2 + 3}{2x_n} \]

通过不断迭代，可以得到根号3的近似值。

3. 十进制逼近：

我们可以直接计算根号3的小数部分，通过不断增加计算的精度，可以得到更加精确的结果。

三、根号3在数学中的应用

根号3在数学中的出现频率非常高，特别是在几何学、三角学和代数学中。

1. 几何构造：

除了在等边三角形中的应用，根号3还出现在其他一些几何构造中。例如，在边长为1的正方形中，对角线长度为根号2，而在边长为1的等边三角形中，高度为根号3除以2。这些构造展示了根号3在几何形状中的基础作用。

2. 三角函数：

在三角函数表中，根号3与60度和30度的三角函数值密切相关。例如，sin(60度) = 根号3除以2，cos(60度) = 1除以2，tan(60度) = 根号3。这些关系使得根号3在解决与角度相关的问题时变得尤为重要。

3. 代数方程：

根号3在解代数方程时经常出现。例如，解方程x^2 = 3可以得到x = 根号3或x = -根号3。这种方程在解决物理和工程问题时非常常见。

四、根号3在物理学中的应用

根号3在物理学中的应用同样广泛，特别是在力学、电磁学和量子力学等领域。

1. 力学：

在力学中，根号3与力的分解和合成密切相关。例如，在解决力的平衡问题时，经常需要用到三角函数，而根号3作为三角函数的一部分，自然会出现在这些问题的解决过程中。

2. 电磁学：

在电磁学中，根号3与电场和磁场的分布有关。特别是在处理均匀带电球体或均匀磁化球体时，根号3会出现在电场强度或磁感应强度的计算公式中。

3. 量子力学：

在量子力学中，根号3出现在波函数的归一化过程中。波函数的归一化要求波函数在整个空间中的积分等于1，这个过程中往往会涉及到根号3的计算。

五、根号3在计算机科学中的应用

在计算机科学中，根号3经常用于图形处理、数值计算和算法设计等领域。

1. 图形处理：

在计算机图形学中，根号3与图形的旋转、缩放和变换等操作有关。特别是在三维图形处理中，根号3会出现在坐标变换和投影矩阵的计算中。

2. 数值计算：

在数值计算中，根号3的近似值可以通过各种算法来计算，如牛顿迭代法、二分法和连续分数法等。这些算法在计算机程序中得到了广泛应用。

3. 算法设计：

在算法设计中，根号3有时作为算法复杂度的一部分出现。例如，在解决某些组合优化问题时，根号3可能会出现在时间复杂度或空间复杂度的计算公式中。

综上所述，根号3作为一个重要的无理数，在数学、物理学和计算机科学等多个领域中都有着广泛的应用。通过对其几何意义、数值计算方法和各领域应用的探讨，我们可以更加深入地理解根号3的重要性和实用性。根号3的值约为1.7320508075688772935274463415059，这一精确数值为我们解决各种问题提供了有力的工具。