探究勾股数的具体值

勾股数是多少？

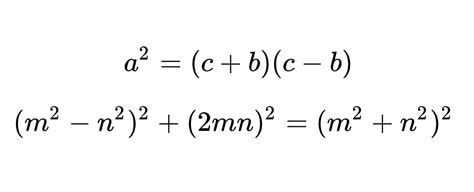
勾股数，这一数学概念，自古以来便在数学、物理学乃至日常生活中占据着举足轻重的地位。它源自勾股定理，即在一个直角三角形中，直角两边的平方和等于斜边的平方。这一简洁而深刻的定理，不仅揭示了直角三角形三边之间的数量关系，还蕴含了丰富的数学规律和美学价值。勾股数，便是这一定理在整数解上的体现，它们以特定的组合方式，展现了数学世界的奇妙与和谐。

一、勾股数的定义与性质

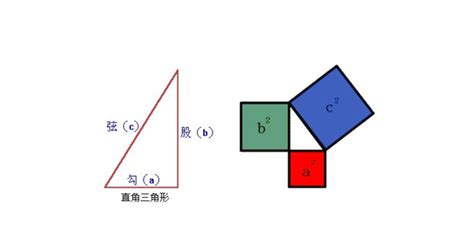
勾股数，通常表示为(a, b, c)，其中a和b是直角三角形的两条直角边，c是斜边，且满足a² + b² = c²。这些数都是正整数，且没有公因数（即它们互质）。例如，(3, 4, 5)便是一组著名的勾股数，因为3² + 4² = 9 + 16 = 25 = 5²。

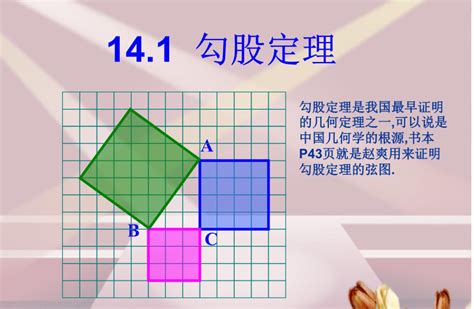
勾股数具有一些有趣的性质。首先，对于任意一组勾股数(a, b, c)，如果k是正整数，那么(ka, kb, kc)也是勾股数。这是因为(ka)² + (kb)² = k²(a² + b²) = k²c² = (kc)²。这一性质表明，勾股数可以无限扩展，形成无数个新的勾股数组合。

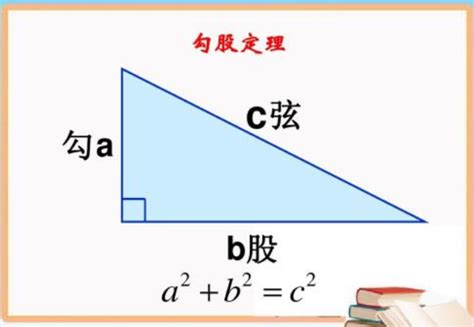
其次，勾股数中的c总是奇数，而a和b则可能同为奇数或一奇一偶。这是因为在任何勾股数(a, b, c)中，如果a和b都是偶数，那么它们的平方和也将是偶数，而c²作为它们的和，也必然是偶数。但c作为斜边，其长度必然大于a和b，因此c本身必然是奇数。反之，如果a和b一奇一偶，那么它们的平方和将是一个奇数加上一个偶数，结果仍然是奇数，这也符合c是奇数的条件。

二、勾股数的生成方法

勾股数的生成方法多种多样，其中一些方法基于数学上的定理和性质，而另一些方法则更加直观和易于理解。

一种常见的生成方法是利用欧几里得算法。欧几里得算法是一种用于计算两个正整数的最大公约数的算法，但它也可以用来生成勾股数。具体来说，我们可以从两个正整数m和n开始（其中m > n且m和n互质），然后计算a = m² - n²，b = 2mn，c = m² + n²。这样得到的(a, b, c)便是一组勾股数。例如，当m = 5，n = 2时，我们可以得到a = 5² - 2² = 21，b = 2 × 5 × 2 = 20，c = 5² + 2² = 29，因此(21, 20, 29)便是一组勾股数。

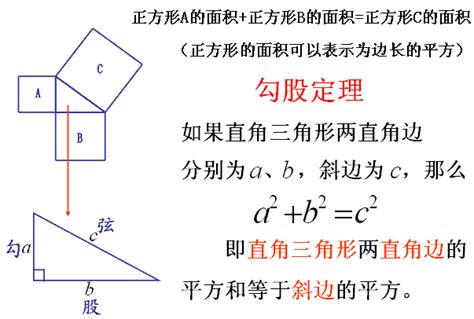
另一种生成方法是基于图形的构造。我们可以构造一个边长为c的正方形，并在其内部绘制四个全等的直角三角形，每个三角形的直角边分别为a和b。这样，正方形的面积便等于四个三角形的面积之和，即c² = 4 × (1/2)ab = 2ab。由于a² + b²也是四个以a和b为边长的正方形的面积之和，因此我们可以得出a² + b² = c²。通过这种方法，我们可以直观地理解勾股数的生成过程。

三、勾股数的应用与意义

勾股数在数学、物理学以及日常生活中都有着广泛的应用和意义。

在数学领域，勾股数是研究整数解和数论问题的重要工具。例如，费马大定理的证明就涉及到了勾股数的性质和规律。此外，勾股数还与椭圆曲线、模形式等现代数学分支有着密切的联系。

在物理学领域，勾股数在力学、光学和电磁学等方面都有着重要的应用。例如，在力学中，我们可以利用勾股定理来计算物体的位移和速度；在光学中，勾股数可以帮助我们理解光的折射和反射规律；在电磁学中，勾股数则与电场和磁场的分布和计算密切相关。

在日常生活中，勾股数的应用同样广泛。例如，在建筑设计中，我们需要利用勾股定理来计算建筑物的尺寸和高度；在导航和定位中，勾股数可以帮助我们确定物体的位置和距离；在航空航天领域，勾股数则与轨道计算和卫星定位等任务息息相关。

四、勾股数的历史与文化价值

勾股数的历史可以追溯到古代文明时期。在中国古代，商高提出了“勾三股四弦五”的勾股定理特例，而《周髀算经》则记载了勾股定理的普遍形式。在西方，古希腊数学家毕达哥拉斯学派最早发现并研究了勾股定理和勾股数。他们认为数是万物的本原，而勾股定理则是数学中最重要的定理之一。毕达哥拉斯学派甚至将勾股定理视为一种神秘的力量，认为它揭示了宇宙间的和谐与秩序。

除了数学价值外，勾股数还具有深厚的文化价值。它不仅是数学史上的一个重要里程碑，也是人类智慧和文明的结晶。勾股数的发现和研究过程充满了探索精神和创新精神，这些精神正是人类不断追求进步和发展的动力源泉。

此外，勾股数还与许多著名的数学家和科学家紧密相连。例如，费马在提出费马大定理时，就涉及到了勾股数的性质和规律；欧拉在研究椭圆曲线时，也发现了与勾股数相关的数学规律。这些数学家的贡献不仅推动了数学学科的发展，也为人类文明的进步做出了重要贡献。

综上所述，勾股数作为数学中的一个重要概念，具有广泛的应用和深远的意义。它不仅揭示了直角三角形三边之间的数量关系，还蕴含了丰富的数学规律和美学价值。通过深入研究勾股数的性质和生成方法，我们可以更好地理解数学世界的奇妙与和谐，也可以为人类文明的进步和发展贡献自己的力量。