求解自然对数底数ln2的值

ln2等于几？一个数学常数的多维度解读

在数学领域中，自然对数（通常以ln表示）是一个极为重要且无处不在的概念。作为对数函数的一种，自然对数以数学常数e（约等于2.71828）为底，具有许多独特的性质和广泛的应用。其中，ln2（即自然对数底为e时，真数为2的对数值）是一个具体的数学常数，它不仅是数学研究中的重要对象，也在物理学、工程学、信息论等多个领域扮演着关键角色。本文将从数学性质、计算方法、应用领域以及文化意义等多个维度，深入探讨ln2这一数学常数的内涵与价值。

数学性质：探索ln2的奥秘

在数学上，ln2具有一系列独特而深刻的性质。首先，它是自然对数函数在x=2处的取值，体现了自然对数函数在实数域上的单调递增性和连续性。由于自然对数函数是实数域上的严格单调递增函数，因此ln2的值是唯一的，且随着x的增大而增大。

其次，ln2与数学中的其他常数和函数存在紧密的联系。例如，它与欧拉数e、圆周率π等著名数学常数共同构成了数学常数家族的成员。此外，ln2还与级数、积分、微分方程等数学工具密切相关，是数学分析中不可或缺的一部分。

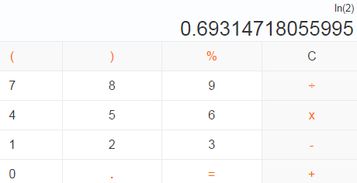
在数值上，ln2的值约为0.69314718056（精确值可无限不循环），这一数值体现了自然对数函数的非线性特征。与有理数和无理数相比，ln2的不可精确表示性使其在数学上更具神秘感和挑战性。

计算方法：求解ln2的多样途径

在计算ln2的值时，数学家们采用了多种方法和技巧。最早的计算方法是通过级数展开或数值积分来实现的。例如，可以利用自然对数的级数定义：

ln(1+x)=x−x22+x33−x44+…|x|<1ln(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \ldots \quad |x| < 1ln(1+x)=x−2x2​+3x3​−4x4​+…∣x∣<1

将x=1代入上述级数中，即可得到ln2的级数展开式：

ln2=1−12+13−14+…\ln 2 = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \ldotsln2=1−21​+31​−41​+…

虽然这一级数收敛较慢，但在古代数学家们已经能够利用它进行粗略的计算。

随着计算技术的发展，现代数学家们采用了更为精确和高效的计算方法。例如，可以利用数值积分的方法来计算ln2的值。通过选择合适的积分区间和被积函数，可以利用计算机进行高精度的数值积分计算，从而得到ln2的近似值。

此外，还可以利用数学软件或编程语言中的内置函数来计算ln2的值。这些函数通常基于高效的数值算法实现，能够在极短的时间内给出高精度的结果。

应用领域：ln2在科学与工程中的价值

ln2作为一个重要的数学常数，在科学与工程中具有广泛的应用价值。在物理学中，ln2与热力学、量子物理等领域密切相关。例如，在热力学中，ln2与熵的概念相联系，可以用来描述系统的无序程度；在量子物理中，ln2则与量子态的叠加、纠缠等现象有关。

在工程学中，ln2同样发挥着重要作用。例如，在通信工程中，ln2与信噪比、信道容量等参数的计算有关；在控制工程中，ln2则与系统的稳定性、响应速度等性能指标的优化有关。

此外，ln2还在信息论、计算机科学等领域中具有广泛的应用。在信息论中，ln2与信息的度量、编码、传输等过程密切相关；在计算机科学中，ln2则与算法的时间复杂度、空间复杂度等性能指标的评估有关。

文化意义：ln2在数学史上的地位

除了在数学、物理学和工程学中的应用外，ln2还具有深厚的文化意义。作为数学史上的一个重要常数，ln2见证了人类对数学和自然规律的不断探索和理解。从古代数学家们对自然对数的初步认识，到现代数学家们对ln2的深入研究和广泛应用，ln2的历史轨迹反映了人类对自然和数学世界的认识不断深化的过程。

此外，ln2还与数学中的其他著名常数和定理存在着千丝万缕的联系。例如，ln2与欧拉公式、费马小定理等著名数学定理密切相关；同时，ln2也是黄金分割比、斐波那契数列等数学概念的延伸和拓展。这些联系不仅丰富了数学宝库的内容，也为我们深入理解和欣赏数学之美提供了新的视角和思路。

结语：ln2——数学与自然的桥梁

综上所述，ln2作为一个重要的数学常数，在数学、物理学、工程学以及文化等多个领域都具有广泛的应用价值和深刻的意义。它不仅体现了自然对数函数的独特性质和广泛应用，也见证了人类对自然和数学世界的不断探索和理解。通过深入研究ln2这一数学常数，我们可以更好地理解数学与自然之间的联系和互动，从而进一步推动数学和科学的发展。

在未来，随着科学技术的不断进步和人类对数学和自然规律的深入理解，我们有理由相信ln2这一数学常数将继续在更多的领域发挥重要作用并为我们带来更多的惊喜和启示。让我们携手共进，在探索数学与自然奥秘的道路上不断前行！