如何用一笔直线将图形分割成两个三角形？

在几何的世界里，简单的线条往往能激发出无限的想象与可能。今天，我们就来探索一个既有趣又富有挑战性的谜题——如何通过“画一条直线变成两个三角形”。这个看似简单的任务，实则蕴含着深刻的几何智慧与创意，它不仅能够激发你的思维活力，还能让你在轻松愉快的氛围中领略到数学的魅力。

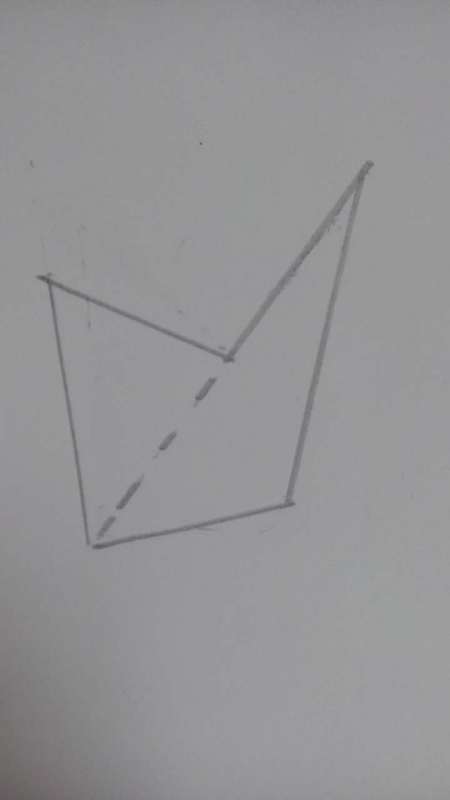
想象一下，你面前有一张空白的纸张，上面没有任何图案或线条。现在，你的任务是仅通过一条直线的绘制，将这片空白区域分割成两个独立的三角形。面对这样的挑战，你是否会感到一丝困惑？毕竟，三角形是由三条边围成的封闭图形，而我们现在只有一条直线的“资源”。但别急，正是这份限制，才使得这个问题变得更加引人入胜。

首先，让我们从几何学的基本原理出发，思考如何巧妙地利用这条直线。在平面上，直线具有无限延伸的特性，但在这个特定的问题中，我们需要关注的是直线如何与潜在的三角形形状相结合。一个关键的思路是，这条直线不仅要切割空间，还要与假想的三角形边界相交，从而创造出两个完整的三角形。

接下来，让我们通过一个逐步推理的过程，揭示这个谜题的答案。假设你已经在心中构想了一个基本的三角形形状，无论是等边、等腰还是不等边三角形，关键在于理解如何通过一条直线将其一分为二。这里，我们可以采用一种逆向思维的方式：先设想两个三角形的形状和位置，然后思考它们之间的共同边界（即你将要绘制的那条直线）会是如何的。

一种常见的解决方案是，选择一个三角形的一个顶点作为起点，然后画一条直线穿过三角形的内部，直至与对边相交。这样，原本的一个三角形就被分割成了两个较小的三角形。但这样的解答显然不够新颖，也不符合我们追求的“一条直线变成两个三角形”的最佳实践。因为我们希望在解答过程中展现出更多的创意和几何美感。

现在，让我们尝试一种更富有想象力的方法。设想你的纸面上有一个隐含的、由虚线构成的三角形框架。这个框架并不真正存在，但它作为我们构思的基础，帮助我们确定直线的最佳路径。在这个虚拟三角形中，选择一条边的中点作为关键节点。从这个节点出发，画一条与这条边垂直且穿过三角形内部的直线。这条直线的神奇之处在于，它不仅能够将原三角形一分为二，而且能够确保分割后的两个部分都是三角形。

为什么这种方法有效呢？原因在于，通过选择边的中点作为起点，并绘制垂直于该边的直线，我们实际上是在创建一个对称的分割。这种对称性不仅保证了分割后的两个部分形状相同（或相似），而且确保了它们都是封闭的三角形。这种解决方案不仅满足了题目的要求，还展示了几何学中对称美的原则。

当然，这个谜题并不只有一种解答方式。通过调整虚拟三角形的形状、大小和位置，以及选择不同的边作为直线绘制的起点，你可以探索出无数种可能的解决方案。每一种方案都代表着一种独特的几何视角和思维方式。

在深入探索这个谜题的过程中，你还会发现一些有趣的几何现象。例如，当你选择一个等腰三角形的底边中点作为起点时，绘制出的直线不仅将三角形分割成两个等腰三角形，还巧妙地展示了等腰三角形中的中线性质——中线与底边平行且等于底边的一半。这种几何性质的展现，无疑为这个问题增添了更多的教育意义和学术价值。

此外，这个问题还可以进一步扩展到三维空间甚至更高维度的几何领域。想象一下，在三维空间中，如何通过一条直线（或更准确地说，一个平面）将一个立方体或四面体分割成两个独立的三棱锥。这样的扩展不仅挑战了我们的空间想象力，还激发了我们对更高维度几何形状的兴趣和探索欲望。

回到我们的原始问题，“画一条直线变成两个三角形”不仅仅是一个简单的几何谜题。它更像是一个启发思考、激发创造力的工具。通过这个问题，我们可以深入探索几何学的奥秘，感受数学中的对称美、简洁美和和谐美。同时，这个问题也提醒我们，在面对困难和挑战时，要保持开放的心态和创新的思维方式。只有这样，我们才能在看似不可能的任务中发现新的可能性，创造出令人惊叹的成果。

所以，下次当你面对一个看似无解的问题时，不妨试着从另一个角度思考它。也许就像我们通过一条直线将空白纸面分割成两个三角形一样，一个简单的想法或方法就能带来意想不到的惊喜和收获。在这个过程中，我们不仅解决了问题，还收获了知识、经验和成长。让我们一起在几何的世界里继续探索吧！